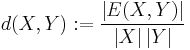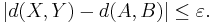Szemerédi regularity lemma
In mathematics, the Szemerédi regularity lemma states that every large enough graph can be divided into subsets of about the same size so that the edges between different subsets behave almost randomly. Szemerédi (1975) introduced a weaker version of this lemma, restricted to bipartite graphs, in order to prove Szemerédi's theorem, and in (Szemerédi 1978) he proved the full lemma. There are several extensions of the regularity lemma to hypergraphs, such as Tao (2006).
Contents |
Formal statement of the regularity lemma
The formal statement of Szemerédi's regularity lemma requires some definitions.
Let G be a graph. The density of a pair of disjoint vertex sets X, Y is the quantity
where E(X,Y) denotes the set of edges having one end vertex in X and one in Y. For ε > 0, a pair of vertex sets X and Y is called ε-pseudo-random, if for all subsets A of X and B of Y satisfying  and
and  , we have
, we have
A partition of the vertex set of G into k sets  is called an ε-regular partition, if
is called an ε-regular partition, if 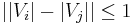 for all i, j, and all except
for all i, j, and all except 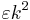 of the pairs
of the pairs 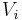 ,
, 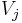 , i < j, are ε-pseudo-random.
, i < j, are ε-pseudo-random.
The Regularity lemma states the following:
It is a common variant in the definition of an ε-regular partition to require that the vertex sets all have the same size, while collecting the leftover vertices in an "error"-set 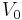 whose size is at most an ε-fraction of the size of the vertex set of G.
whose size is at most an ε-fraction of the size of the vertex set of G.
The bound M for the number of parts in the partition of the graph given by the proofs of Szemeredi's regularity lemma is very large, given by a log(1/ε5)-level iterated exponential of m. At one time it was hoped that the true bound was much smaller, which would have had several useful applications. However Gowers (1997) found examples of graphs for which M does indeed grow very fast and is at least as large as a log(1/ε)-level iterated exponential of m. In particular the best bound has level exactly 4 in the Grzegorczyk hierarchy, and so is not an elementary recursive function.
Extensions
Komlós, Sárközy and Szemerédi later proved in the blow-up lemma that the regular pairs in Szemerédi regularity lemma behave like complete bipartite graphs under the correct conditions. The lemma allowed for deeper exploration into the nature of embeddings of large sparse graphs into dense graphs.
See also
References
- Gowers, W. T. (1997), "Lower bounds of tower type for Szemerédi's uniformity lemma", Geometric and Functional Analysis 7 (2): 322–337, doi:10.1007/PL00001621, MR1445389
- Gowers, W. T. (2007), "Hypergraph regularity and the multidimensional Szemerédi theorem", Annals of Mathematics. Second Series 166 (3): 897–946, doi:10.4007/annals.2007.166.897, MR2373376
- Komlós, János; Miklos Simonovits: Szemerédi's regularity lemma and its applications in graph theory. Combinatorics, Paul Erdös is eighty, Vol. 2 (Keszthely, 1993), 295-352, Bolyai Soc. Math. Stud., 2, János Bolyai Math. Soc., Budapest, 1996.
- Komlós, János; Shokoufandeh, Ali; Simonovits, Miklós; Szemerédi, Endre (2002), "The regularity lemma and its applications in graph theory", Theoretical aspects of computer science (Tehran, 2000), Lecture Notes in Comput. Sci., 2292, Berlin, New York: Springer-Verlag, pp. 84–112, doi:10.1007/3-540-45878-6_3, MR1966181
- Szemerédi, Endre (1975), "On sets of integers containing no k elements in arithmetic progression", Polska Akademia Nauk. Instytut Matematyczny. Acta Arithmetica 27: 199–245, MR0369312, http://matwbn.icm.edu.pl/tresc.php?wyd=6&tom=27
- Szemerédi, Endre (1978), "Regular partitions of graphs", Problèmes combinatoires et théorie des graphes (Colloq. Internat. CNRS, Univ. Orsay, Orsay, 1976), Colloq. Internat. CNRS, 260, Paris: CNRS, pp. 399–401, MR540024
- Tao, Terence (2006), "A variant of the hypergraph removal lemma", Journal of Combinatorial Theory. Series A 113 (7): 1257–1280, arXiv:math.CO/0503572, doi:10.1016/j.jcta.2005.11.006, MR2259060